Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Geschwindigkeit und Beschleunigung
Berechnung von Geschwindigkeit und Beschleunigung
Die Geschwindigkeit v gibt an, wie rasch man von einem Ort zu einem anderen gelangen kann. Die Bestimmung der Geschwindigkeit benötigt eine Größe (Zahlenwert mit Dimension) und eine Richtung.
Die Beschleunigung a gibt an, wie rasch sich dabei die Geschwindigkeit ändert. Auch zur Bestimmung der Beschleunigung ist sowohl die Größe als auch die Richtung nötig.
Berechnung der Geschwindigkeit
s₁ … Ort zum Zeitpunkt t₁
s₂ … Ort zum Zeitpunkt t₂
Der Ort wird zu Beginn als Null angenommen (s₁ = 0).
Genaugenommen wird immer eine Durchschnittsgeschwindigkeit während des betrachteten Zeitintervalls bestimmt. Je kürzer der Zeitraum ist, desto genauer bestimmt man eine Momentangeschwindigkeit.
Berechnung der Beschleunigung
v₁ … Geschwindigkeit zum Zeitpunkt t₁
v₂ … Geschwindigkeit zum Zeitpunkt t₂
Die Geschwindigkeit ist zu Beginn Null (v₁ = 0).
Richtung
Geschwindigkeit und Beschleunigung haben eine Richtung. Wird die Geschwindigkeit größer, spricht man von positiver Beschleunigung. Die Beschleunigung zeigt dabei in Bewegungsrichtung. Wird die Geschwindigkeit kleiner, nennt man dies negative Beschleunigung oder Verzögerung. Die Richtung der Beschleunigung zeigt gegen die Bewegungsrichtung. Bereits die Änderung der Richtung der Geschwindigkeit, ohne Änderung der Größe, ist eine Beschleunigung.
Da die Einheit der Geschwindigkeit 1 m/s beträgt, ergibt sich für die Beschleunigung die Einheit 1 m/s pro s oder 1 m/s².

Hier gäbe es mehr!
Schnelle Autos
Gleichmäßig beschleunigte Bewegung
Beschleunigung eines Autos
Bei einer gleichmäßig beschleunigten Bewegung ist die Beschleunigung a immer gleich groß (konstant). Das heißt, die Geschwindigkeit erhöht sich in jeder Sekunde um den gleichen Betrag. Bei bekannter Beschleunigung kann man die Geschwindigkeit zu jedem Zeitpunkt berechnen.
Man erhält die Endgeschwindigkeit v zum Zeitpunkt t mithilfe folgender Formel:
v = a · t
Beschleunigung eines Autos
Ein Auto startet mit einer Beschleunigung von 3 m/s². Es hat nach 6 Sekunden eine Geschwindigkeit v = 3 m/s² · 6; s = 18 m/s.
Der zum Zeitpunkt t zurückgelegte Weg kann mithilfe folgender Formel berechnet werden:
Das Auto im Beispiel oben fährt m = 52 m weit.

Schnellbremsung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Mittelklassewagen erreichen bei trockener Straße eine Bremsbeschleunigung von a = 6 m/s²
Wie schnell kann ein solcher Wagen von 100 km/h auf Null bremsen?
Aus v = a · t folgt zur Berechnung der Zeit
Die Geschwindigkeit muss zuerst in m/s umgewandelt werden.
v = 27,8 m/s;
Wie weit fährt der Wagen dabei?
Weg
Für t wird das Ergebnis von vorhin eingesetzt.

Diesen langen Bremsweg muss man im Straßenverkehr berücksichtigen.
Training
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Wahr oder falsch?
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Wie schnell war Usain Bolt?
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Usain Bolts Beschleunigung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Usain Bolts Durchschnittsgeschwindigkeit
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Durchschnittsgeschwindigkeit bei einem Marathonlauf
Bewegungsdiagramme
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
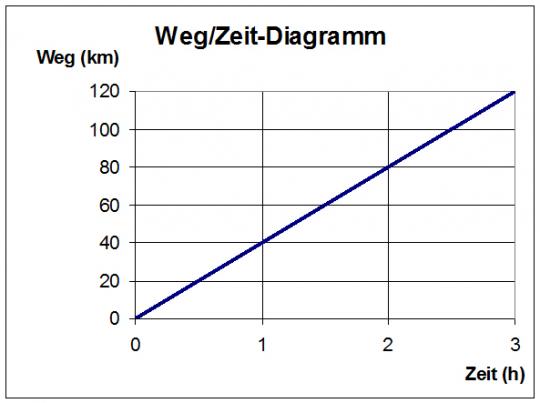
Das Weg/Zeit-Diagramm (s/t-Diagramm) eines Fahrzeugs, das sich mit 40 km/h gleichmäßig bewegt, zeigt das untenstehende Bild.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Erstelle ein Bewegungsdiagramm für ein Fahrzeug, das sich mit 20 km/h bzw. mit 50 km/h bewegt. Du kannst dafür die PDF-Vorlage ausdrucken.
Gib vor Erstellung der Zeichnung an, wie steil die Strecken verglichen mit der gezeigten oben (bei 40 km/h) verlaufen werden.
Gleichmäßig beschleunigte Bewegung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
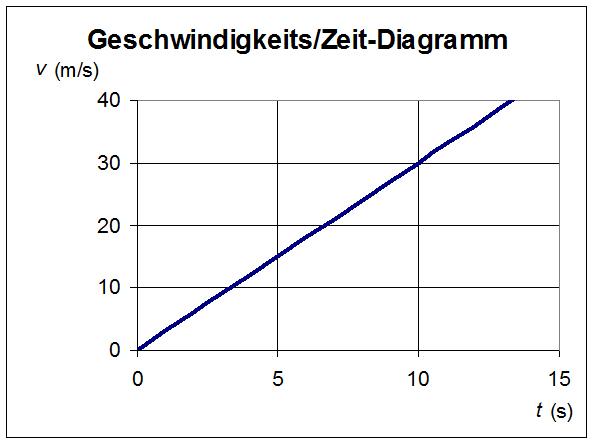
Das Bild zeigt ein Geschwindigkeit/Zeit-Diagramm (v/t-Diagramm) eines Autos, das sich mit der Beschleunigung 3 m/s² bewegt. Nach 10 s beträgt die Geschwindigkeit 30 m/s.

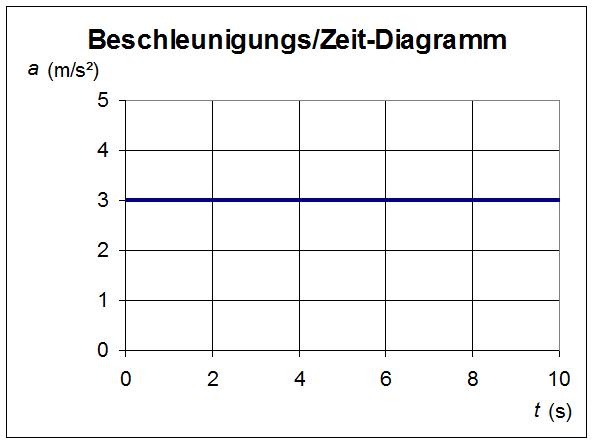
Ist die Beschleunigung konstant, ergibt sich im Beschleunigung/Zeit-Diagramm (a/t-Diagramm) eine Strecke parallel zur Zeitachse.

Der Weg bei einer gleichmäßig beschleunigten Bewegung wird durch die Formel berechnet.

Zur Erstellung des Weg/Zeit-Diagramms müsste man in kleinen Zeitschritten immer wieder den Weg berechnen und dann in das Diagramm eintragen. Man kann aber auch einfach die Formel in ein entsprechendes Programm eintragen und erhält dann die Zeichnung.
Das Ergebnis siehst du in der Abbildung.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.

Lies aus dem Diagramm im Bild oben rechts den Weg nach 4 s, 6 s und 8 s heraus.
Überprüfe das Ergebnis durch Berechnung.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
v/t- & s/t-Diagramm
vtst_diagramm.pdf · 122 kB
Drucke das PDF aus und erstelle für die Beschleunigung a = 4 m/s² das v/t- und das s/t-Diagramm.
Ferngesteuertes Auto
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Oskar hat am Boden alle zwei Meter eine Markierung gezeichnet. Dann lenkt er sein ferngesteuertes Auto geradlinig über die Markierungen und misst die Zeiten, an denen das Auto die Markierungen passiert. Seine Aufzeichnungen sehen so aus:
Meter: 0; 2; 4; 6; 8; 10
Zeiten (s): 0; 1,8; 3,2; 4,7; 6,2; 7,6
Ferngesteuertes Auto
ferngesteuertes_auto.pdf · 35 kB
Diskutiert in der Klasse, ob bzw. wie man diese Daten übersichtlicher anschreiben könnte.
Besprich mit deiner Sitznachbarin, deinem Sitznachbarn, wie man zeigen könnte, ob sich das Auto gleichmäßig oder gleichmäßig beschleunigt bewegt hat.
Zeichne ein s/t-Diagramm und ein v/t-Diagramm. Du kannst dazu die PDF-Vorlage verwenden.
Berechne die durchschnittliche Geschwindigkeit des Autos.
Berechne die Durchschnittsgeschwindigkeiten des Autos in den einzelnen Intervallen (von 0 bis 2 m, von 2 m bis 4 m …).
Überlege, welche Gründe es geben kann, dass sich die Geschwindigkeiten in den Intervallen von der gesamten Durchschnittsgeschwindigkeit unterscheiden.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Diagramme mit Excel
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Bewegungsdiagramm
gpt4s76z8_IKT_bewegungsdiagramm.xlsx · 9 kB
Verwende Excel!
Öffne die Vorlage, finde die richtigen Formeln für die Spalten C und F und füge passende Diagramme ein.
Merke
Beschleunigung – Zusammenfassung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Die Änderung der Geschwindigkeit in einem bestimmten Zeitraum wird Beschleunigung genannt.
Die Einheit der Beschleunigung ist 1 m/s2.
Bei einer gleichmäßig beschleunigten Bewegung ergibt sich die Geschwindigkeit aus v = a ∙ t und der Weg aus .