Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Kraft und Beschleunigung
Kraft, Masse und Beschleunigung
Zu jeder Änderung der Geschwindigkeit wird eine Kraft benötigt. Der Motor eines Autos erzeugt diese Kraft zum Beschleunigen.

KFZ-Motor
Der Motor eines Ford Fiesta, Baujahr 2001.
- Je größer die Masse des Fahrzeugs ist, desto größer muss auch die Kraft sein.
- Je größer die Beschleunigung sein soll, desto größer muss die Kraft sein. Autos, die besonders schnell auf 100 km/h beschleunigen sollen, müssen daher viel Kraft zur Verfügung stellen.
Kraft = Masse mal Beschleunigung (F = m · a)
Wirkt auf einen Körper eine Kraft, so wird dieser Körper beschleunigt. Jede Beschleunigung wird durch eine Kraft verursacht.
Kraft und Beschleunigung zeigen in die gleiche Richtung.
Wirkt eine Kraft auf einen Körper, so kommt es zu dessen Beschleunigung.
Umgekehrt beruht jede Beschleunigung auf einer Krafteinwirkung.
Die Krafteinheit 1 Newton (1 N) ist die Kraft, die man benötigt, um einer Masse von 1 kg eine Beschleunigung von 1 m/s² zu erteilen.
Beispiel Motorkraft
Jemand beschleunigt mit seinem Auto von 0 auf 100 km/h in 10 Sekunden. Welche Kraft muss der Motor dafür aufbringen, wenn die Masse von Auto und Fahrer 1 000 kg beträgt?
Beschleunigung:
Kraft:
Nun ist das Auto vollbesetzt, die 4 zusätzlichen Personen haben eine Masse von 320 kg.
Welche Beschleunigung kann der Motor dem Auto jetzt verleihen?
Aus F = m · a erhält man
Welche Geschwindigkeit hat das Auto jetzt nach 10 Sekunden?
Aus v = a · t erhält man mit a = 2,1 m/s² die Geschwindigkeit v = 2,1 · 10 m/s = 21 m/s = 76 km/h.
Saturnrakete
Hier gäbe es mehr!

Eine Saturnrakete hat beim Start eine Masse von etwa 3 000 Tonnen. Die fünf Triebwerke erzeugen einen Schub von 34 Millionen N.
Berechne, welche Beschleunigung die Rakete zu Beginn des Starts hat. Runde das Ergebnis auf eine Dezimalstelle!
Kraft beim Bremsen
Welche Kraft entsteht beim Bremsen?
Beim Bremsen treten große Kräfte auf, die oftmals zu wenig berücksichtigt werden. In Kraftfahrzeugen ist das Anlegen von Sicherheitsgurten vorgeschrieben, damit beim Bremsen die Passagiere nicht nach vorne geschleudert werden.
Beispiel
Ein Auto fährt mit 7 km/h auf ein Hindernis auf.
Wie viel Kraft muss der Gurt bei einer Person mit der Masse 80 kg aufnehmen, wenn der Aufprall in 1/10 Sekunde erfolgt?
Dazu wird zunächst die Beschleunigung berechnet.
Diese ergibt sich aus der Formel v = a · t durch Umformung mit .
Die Geschwindigkeit muss man in m/s umrechnen.
Bremsbeschleunigung:
Die auftretende Kraft erhält man nun mithilfe der Formel F = m · a.
Kraft: F = m · a = 80 · 20 N = 1 600 N
Diese Kraft entspricht dem Gewicht eines Körpers mit 160 kg.
Gurteschlitten
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Gerade in der Stadt verzichten Leute oft aufs Angurten, weil sie glauben, dass sie sich bei den geringen Geschwindigkeiten noch mit den Händen abstützen und auffangen können. Autofahrerklubs und Unfallversicherungsgesellschaften versuchen, die Leute mithilfe eines Gurteschlittens vom Gegenteil zu überzeugen. Der Gurteschlitten simuliert einen Aufprall mit etwa 7 km/h. Ein solcher Versuch hat schon viele Leute davon überzeugt, dass man die auftretenden Kräfte nicht mit den Händen auffangen kann.

Gefährliche Geschoße
Im Auto unbefestigt liegende Gegenstände können beim Bremsen zu gefährlichen Geschoßen werden.

Beispiel
Ein Auto fährt mit 50 km/h gegen ein Hindernis. Die Bremsbeschleunigung beträgt dabei etwa 500 m/s². Erfährt eine im Auto liegende Getränkedose (Masse 0,33 kg) ebenfalls diese Bremsbeschleunigung, so übt sie folgende Kraft aus:
F = m · a = 0,33 · 150 N = 165 N
Diese Kraft entspricht dem Gewicht von etwa 50 Dosen.

Training
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Setze die Silben richtig zusammen!
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Kräfte
kraefte.pdf · 97 kB

Drucke das PDF aus und zeichne in die vier Figuren die Kräfte ein, die jeweils auf das Buch, die Kugel und die Hantel wirken.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
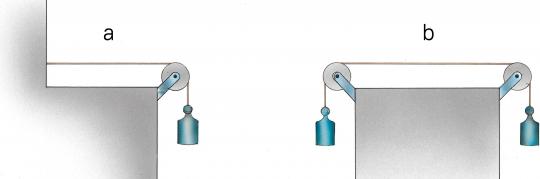
Schnurspannung
Überlegt in der Klasse, ob die Kraft, die die Schnur spannt, im Fall a gleich groß ist wie im Fall b.
Begründung:
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Motorkraft
Oskar hat bei seinem ferngesteuerten Auto gemessen, dass es vom Start weg bis zu einer Entfernung von 2 Metern 1,8 Sekunden benötigt hat.
Berechne die dafür verwendete Motorkraft, wenn das Auto eine Masse von 80 dag hat.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Wahr oder falsch?
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Abstützen
In der Fahrschule
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.

wird manchmal folgende Formel für die Berechnung des Bremswegs s verwendet:
Dividiere die Geschwindigkeit, angegeben in Kilometer pro Stunde, durch zehn und quadriere das Ergebnis.
Die exakte Formel lautet
Berechnung mit der Fahrschul-Formel:
Berechnung mit der exakten Formel:
Diskutiert in der Klasse, warum eine andere Formel verwendet wird. Diskutiert auch, ob der Unterschied der Ergebnisse wichtig ist.
Berechne die Bremskraft auf eine Person mit einer Masse von m = 70 kg nach beiden Formeln.
Vollbremsung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Karla fährt im Ortsgebiet mit ihrem PKW mit 50 km/h. Plötzlich sieht sie einen Hund auf ihrer Fahrbahn laufen. Sie reagiert sehr schnell, steigt kraftvoll auf die Bremse und kommt in 3,5 Sekunden zum Stehen.
Berechne, mit welcher Kraft Karla, die eine Masse von 60 kg hat, in die Sitzgurte geworfen wird.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Elektrofahrzeug
Ein modernes Elektroauto hat eine Masse von 1,9 Tonnen und kann mit einer Kraft von 13 000 N beschleunigen.
Berechne die Geschwindigkeit nach 2 s.
Bremsweg
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
So kommt man zur Formel für den Bremsweg.
Aus der Formel für die Geschwindigkeit bei gleichbleibender Beschleunigung v = a · t ergibt sich .
Setzt man dies in die Formel für den Weg ein, so erhält man für den Weg bei einer gleichmäßig beschleunigten Bewegung .
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Knautschzone
Sturmgewehr
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.

Beim Sturmgewehr des österreichischen Bundesheeres StG 77 erreicht das Geschoß eine Geschwindigkeit von 990 m/s. Der Lauf des Gewehres hat eine Länge von 407 mm und das Geschoß besitzt eine Masse von 13 g.
Berechne die Beschleunigung des Geschoßes.
Berechne die Kraft, mit der das Geschoß beschleunigt wird.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Start eines Jumbo-Jets
Merke
Kraft – Zusammenfassung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Zu jeder Geschwindigkeitsänderung wird eine Kraft benötigt. Diese Kraft hängt von der Masse und der Beschleunigung ab: $F = m · a$
1 Newton ist die Kraft, die man benötigt, um einer Masse von 1 kg eine Beschleunigung von 1 m/s² zu erteilen.