Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Planeten und Satelliten
Inhalt
Fallen ohne Ende
Die Gravitationskraft der Erde
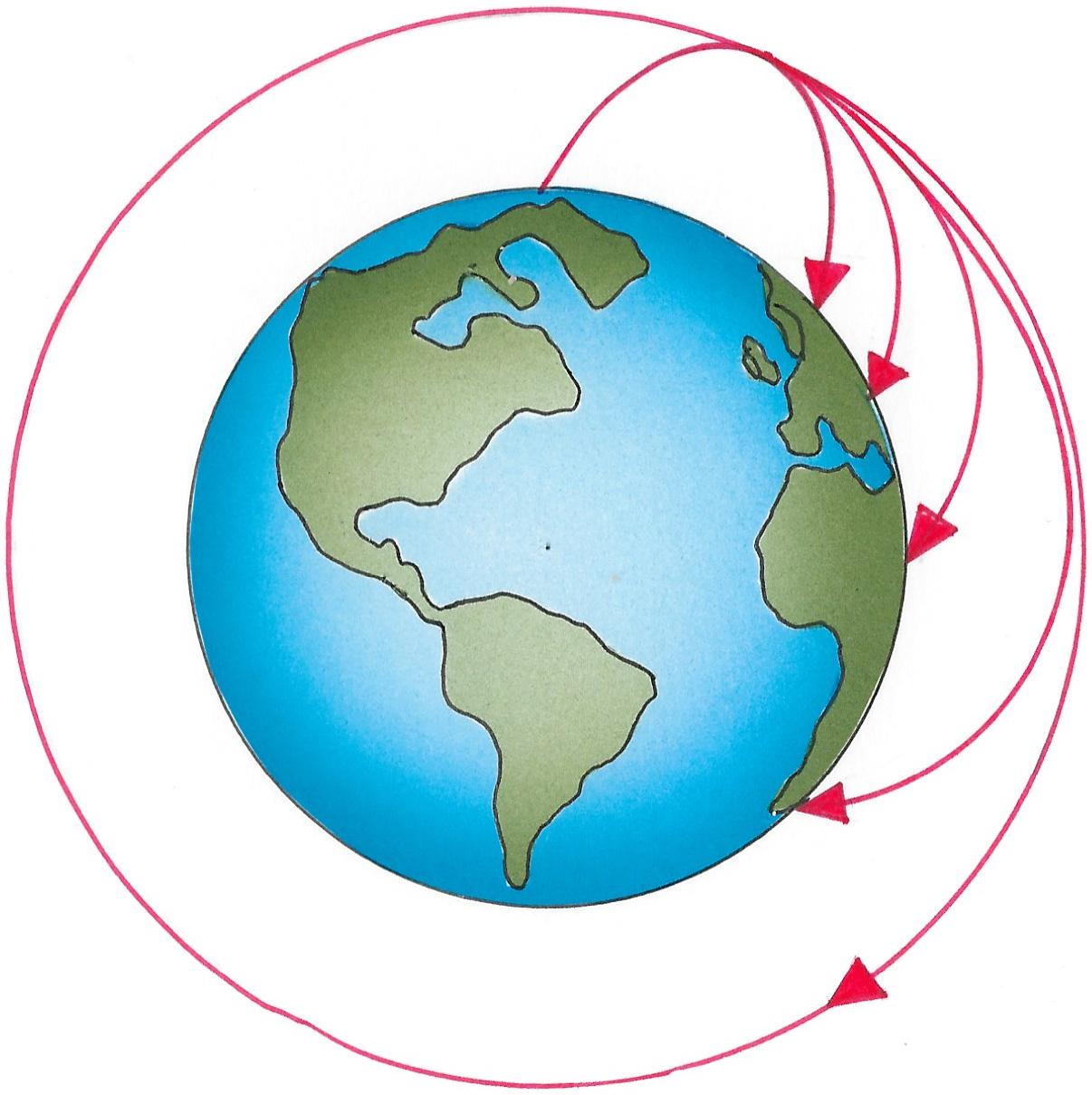
Wirft man einen Körper schräg in die Höhe, so fällt er aufgrund seiner Schwerkraft wieder auf die Erde zurück. Wirft man ihn stärker, fliegt er weiter. Nun kann man den Körper mit einer solchen Geschwindigkeit abfeuern, dass er nicht mehr auf die Erde zurückfällt, sondern in eine kreisförmige Bahn um die Erde gerät. Der Körper fällt also andauernd um die Erde herum.
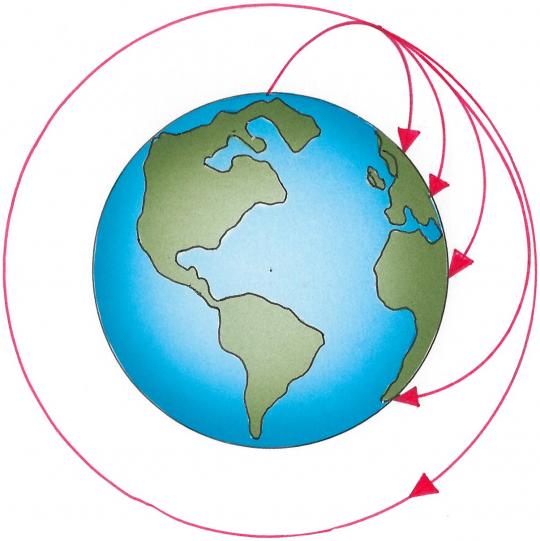
Aufgrund der Trägheitsbewegung würde sich der Körper geradlinig weiterbewegen und von der Erde entfernen. Die Gravitationskraft lässt ihn gleichzeitig zur Erde hin fallen. Die Gravitation als Zentripetalkraft zwingt den Körper zu der Kreisbahn.
Auf ähnliche Weise ergeben sich die Bahnen vieler Himmelskörper.
Die Bewegungen von Satelliten oder Raumstationen entsprechen einem nicht endenden freien Fallen. Eine Astronautin oder ein Astronaut scheint in der Raumkapsel zu schweben, in Wirklichkeit fällt sie bzw. er gleich schnell wie die Raumkapsel.

Satelliten bewegen sich in kreisähnlichen elliptischen Bahnen um die Erde. Um z. B. Fernsehprogramme zur Erde senden zu können, ist es nötig, dass sich der Satellit immer am selben Punkt über der Erde befindet (geostationärer Satellit). Der Satellit muss also genauso lang für die Umrundung der Erde brauchen wie die Erde für eine volle Umdrehung um ihre Achse (24 Stunden).
Der Mond kreist genauso um die Erde wie ein Satellit.

Fluchtgeschwindigkeit
Hier gäbe es mehr!
Damit ein Satellit auf einer Umlaufbahn kreisen kann, muss er eine Geschwindigkeit von 7,9 km/s haben. Um die Erdumlaufbahn zu verlassen und ins Weltall zu fliegen, benötigt der Satellit eine Geschwindigkeit von 11,2 km/s. Diese Geschwindigkeit heißt Fluchtgeschwindigkeit.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Rechne die beiden Geschwindigkeiten in km/h um.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Berechne, wie lange ein Satellit 400 km über der Erdoberfläche für eine Umrundung der Erde braucht. Der Erdradius beträgt 6 370 km.
Drücke das Ergebnis in Stunden aus. Runde auf 2 Dezimalstellen.
Planetensystem
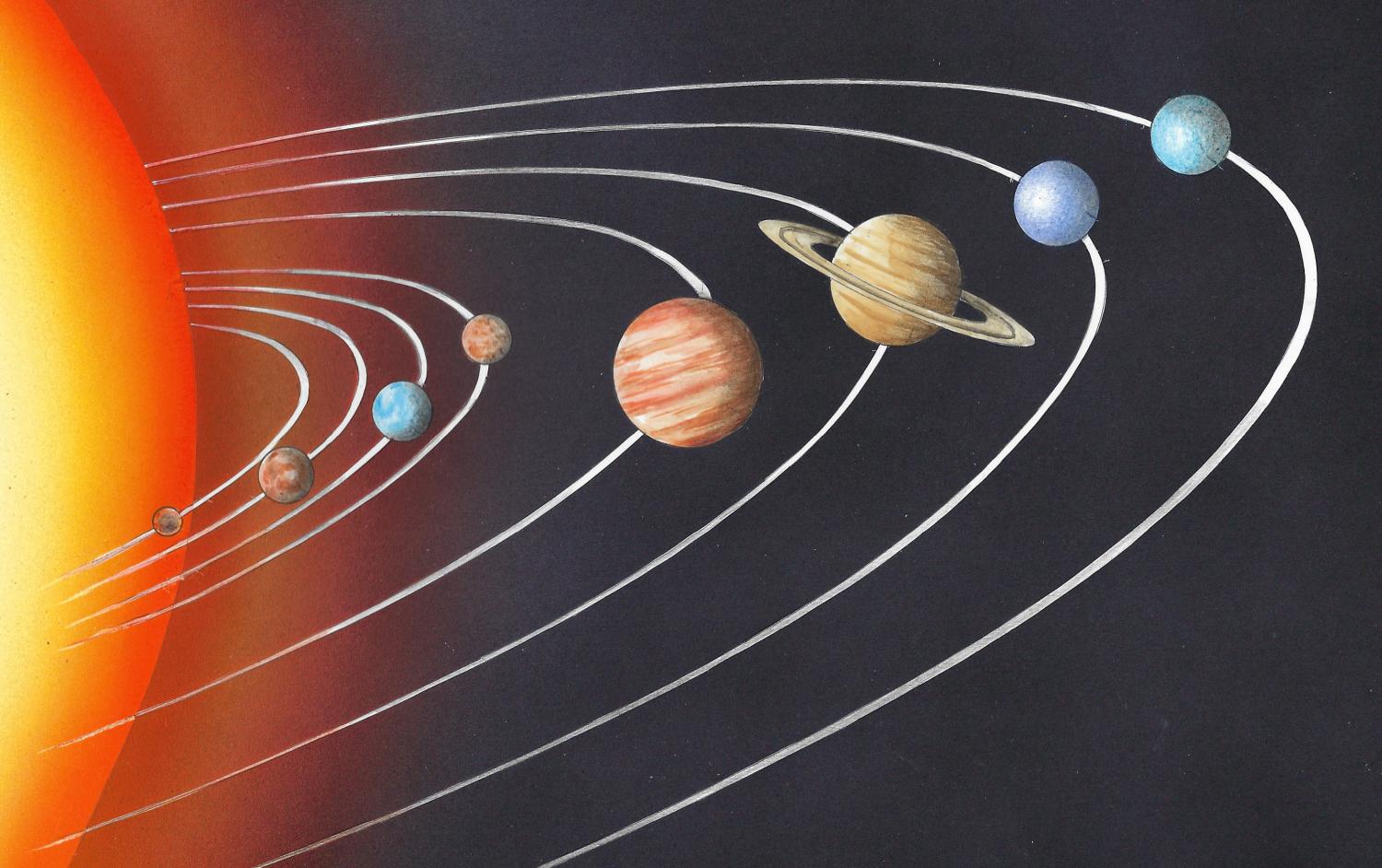
Planeten im Sonnensystem
Die Planeten bewegen sich um die Sonne, wie sich der Mond um die Erde bewegt. Die Bahnen sind Ellipsen. Diese Erkenntnis geht auf Johannes Kepler zurück. Er formulierte drei Gesetze über die Bahnen und Umlaufzeiten der Planeten.
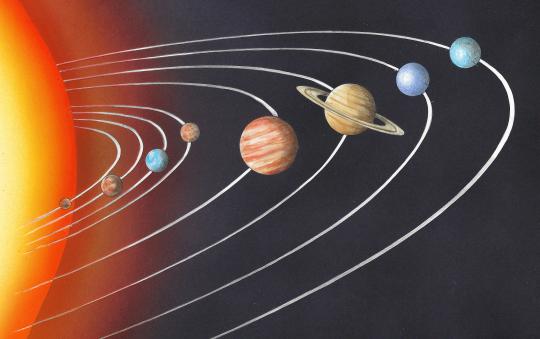
Unser Sonnensystem in Zahlen
Unser Sonnensystem
Die Zahlen kannst du dir auch in einer Tabelle ansehen.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Suche Informationen über Johannes Kepler und schreibe die wichtigsten Daten auf.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Pluto
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Bis 2006 bestand unser Sonnensystem aus neun Planeten. Da aber immer mehr Himmelskörper in etwa der Größe des Pluto entdeckt wurden, zählt man seither Pluto zu den Kleinplaneten.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Finde heraus, nach wem Pluto benannt ist.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
| Planet | Durchmesser (in km) | Mittlere Entfernung von der Sonne (in Mio. km) |
|---|---|---|
| Merkur | 4 878 | 58 |
| Venus | 12 104 | 108 |
| Erde | 12 742 | 150 |
| Mars | 6 780 | 228 |
| Jupiter | 139 822 | 778 |
| Saturn | 116 464 | 1 428 |
| Uranus | 50 724 | 2 873 |
| Neptun | 49 248 | 4 502 |
| Durchmesser der Sonne: 1 391 400 km |
Planeten
In der Tabelle sind einige Daten der Planeten unseres Sonnensystems zusammengestellt.
Gib an, welche benachbarten Planeten die größte Entfernung voneinander aufweisen.
Welche sind sich am nächsten?
Klassenprojekt Planetenweg
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Die Abstände der Planeten von der Sonne sollen im Schulhaus und/oder im Schulhof sichtbar gemacht werden. Dazu sollen die Abstände in den richtigen Verhältnissen am Boden oder an der Wand angezeigt werden. Berechne, wie groß die Sonne und die Planeten in diesem Maßstab sind.
Überlegt, wie man dieses Projekt realisieren könnte.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Training
Raumschiff ans Ziel bringen
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Sucht ein Handyspiel, bei dem man ein Raumschiff an ein Ziel bringen muss.
Welche habt ihr gefunden?
Mit welchen Schwierigkeiten müsst ihr als Raumschiff-Piloten kämpfen?
Planeten ordnen
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Plastikflasche
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.

Bohre eine Plastikflasche unten an, sodass Flüssigkeit aus den Löchern ausfließen kann (siehe Abbildung). Fülle die Flasche mit Wasser und halte sie in die Höhe.
Lass dann die Flasche fallen und beobachte dabei die Wasserstrahlen.
Beschreibe deine Beobachtung. Begründe.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Richtig oder falsch?
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Hier sind Wortteile von Begriffen aus dieser Einheit durcheinandergekommen.
Bilde die richtigen Wörter und schreibe zu jedem Begriff eine Frage.
Fluchtbahn
Frage:
Umlaufbewegung
Frage:
Trägheitsstation
Frage:
Raumkraft
Frage:
Kreiszeit
Frage:
Schwergeschwindigkeit
Frage:
Schaumgummi
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Lege einen schweren Gegenstand auf eine dicke Schaumgummiunterlage, sodass diese sichtbar eingedrückt wird.
Lass dann die Anordnung fallen und beobachte den Schaumgummi.
Beschreibe deine Beobachtung. Begründe.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Wort-Suchrätsel
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Wähle fünf Begriffe aus und schreibe einen kurzen Satz, der den jeweiligen Begriff erklärt, auf.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Lies die Infotexte weiter oben. Ordne die folgenden Sätze in der Reihenfolge, in der sie vorkommen.
- Der Körper fällt also andauernd um die Erde herum.
- Die Bahnen sind Ellipsen.
- Ein Körper kann sich aufgrund der gegenseitigen Gravitationsanziehung um einen anderen bewegen – genaugenommen um den gemeinsamen Schwerpunkt.
- Die Bewegungen von Satelliten oder Raumstationen entsprechen einem nicht endenden freien Fallen.
- Diese Geschwindigkeit heißt Fluchtgeschwindigkeit.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Kräfte bei Satelliten
satellit.pdf · 290 kB
Drucke das PDF aus und zeichne die Kraft ein, die auf den Satelliten wirkt.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Fluchtgeschwindigkeit
Eine Rakete hat beim Start eine Beschleunigung von a = 12 m/s².
Berechne, wie lange es dauert, bis die Rakete mit dieser Beschleunigung die Geschwindigkeit von 7,9 km/s erreicht, die für eine Umlaufbahn nötig ist.
Um ins Weltall zu fliegen, muss die Rakete die Fluchtgeschwindigkeit von 11,2 km/s haben. Berechne, wie lange sie braucht, um diese Geschwindigkeit zu erreichen.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Finde heraus,
welche Planeten man zu den erdnahen Planeten zählt …
… und ob sie eine Gasatmosphäre haben.
Beurteile, ob wir in dieser Atmosphäre leben könnten.
Keplersche Gesetze
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Keplersches Gesetz
Die Planetenbahnen sind Ellipsen mit der Sonne in einem Brennpunkt.
2. Keplersches Gesetz
Die Verbindungslinie Planet-Sonne (Fahrstrahl) überstreicht in gleichen Zeiten gleich große Flächen.
Der Planet bewegt sich also unterschiedlich schnell. In Sonnennähe ist der Planet schneller als in Sonnenferne.
3. Keplersche Gesetz
Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die dritten Potenzen ihrer großen Halbachsen.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Erkläre, was man unter dem geozentrischen Weltbild versteht.
Gib an, wer es durch das heliozentrische Weltbild abgelöst hat.
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Schau dir im Internet eine Animation zum 2. Keplerschen Gesetz an.
Erkläre, was man unter „Perihel“ und „Aphel“ versteht.
Perihel:
Aphel:
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
| Planet | Umlaufzeit | Große Halbachse (in Einheiten des Erdbahnradius) |
|---|---|---|
| Merkur | 88 Tage | 0,39 |
| Venus | 224,7 Tage | 0,72 |
| Erde | 365,3 Tage | 1 |
| Mars | 1,9 Jahre | 1,52 |
| Jupiter | 11,9 Jahre | 5,2 |
| Saturn | 29,4 Jahre | 9,5 |
| Uranus | 84 Jahre | 19,2 |
| Neptun | 165 Jahre | 30 |
Drittes Keplersches Gesetz
gpt4s87z12_IKT_drittes_keplersches_gesetz.xlsx · 9 kB
Überprüfe das 3. Keplersche Gesetz mithilfe der in der Tabelle angegebenen Daten für zwei Planeten, z. B. Merkur und Erde. Dazu musst du die Quadrate der Umlaufzeiten und die dritten Potenzen der Halbachsen bilden. Bilde dann den Quotienten der Quadrate und der dritten Potenzen.
Beachte, dass die Umlaufzeiten der ersten drei Planeten in Tagen, die der anderen in Jahren angegeben sind.
Du bist nicht angemeldet.
Registriere dich oder melde dich an, um deinen Text zu dieser Aufgabe zu speichern.
Excel verwenden
Löse das Beispiel mit Excel! Du kannst dabei das Erstellen von Formeln gut üben.
Verwende die Vorlage!
Merke
Planeten und Satelliten – Zusammenfassung
Hier gäbe es mehr!
Mit einem Plus- oder Premium-Zugang kannst du dieses Element ansehen.
Ein Körper kann sich aufgrund der gegenseitigen Gravitationsanziehung um einen anderen bewegen – genaugenommen um den gemeinsamen Schwerpunkt. Diese Bewegung trifft auf Satelliten, den Mond, aber auch auf Planeten oder Kometen zu.